解释太阳能量来源《张朝阳的物理课》估算太阳

琴弦的振动是怎样的形式？声音在空气中的传播速度如何计算？太阳的寿命大约还剩50亿年？4月8日，《张朝阳的物理课》线下第二课开讲，搜狐创始人、董事局主席兼CEO张朝阳与来自北京各高校的物理学子及物理学爱好者们一起探讨物理的奥秘。课堂上，他陆续讲解了经典波动方程的推导与声速的计算，之后又与现场同学交流探讨了太阳内部的核反应、太阳寿命的估算，以及宇宙大爆炸理论的两个实验证据等物理问题。

推导经典波动方程 从琴弦振动开始

本节线下课，张朝阳先介绍了琴弦振动方程的推导。以琴弦初始位置建立x轴，弦的振动方向为u轴。采用平面运动模型并假设琴弦只能沿一个方向振动，这样就把三维问题简化成了二维问题。弦在某一时刻的位置用u(x,t)描述，它表示弦对平衡位置的偏离。

在课程中，假设弦的振动比较微小，u(x,t)对x的偏导数远远小于1。假设琴弦在初始位置的质量线密度为μ，考虑在区间(x,x+Δx)上琴弦的微元的运动。忽略重力，那么这部分微元只受到弦自身张力的作用。

推导过程中，暂且假设弦的张力T处处相等。需要说明的是，因为弦只沿u方向振动，不沿x方向运动，所以微元受到的x方向的合力为零，于是张力在x轴上的分量Tx处处相等，而u方向的张力Tu不是处处相等的，从而T实际上不是处处相等的。不过，因为接下来的推导需要的是Tu，当u(x,t)对x的偏导数远远小于1时，无论使用T还是Tx来估算Tu，最低阶近似都是一样的，所以可以假设T为常数。而当u(x,t)对x的偏导数不是小量时，则须使用Tx为常数来推导，此时依然能得到严格的波动方程。

由于u(x,t)对x的偏导数远远小于1，于是弦的切线倾角θ非常小，所以Tu约等于T乘以θ，而θ可以用u(x,t)对x的偏导数来近似，于是微元受到的u方向的合力为：

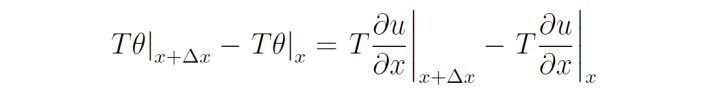
利用牛顿第二定律，可得：

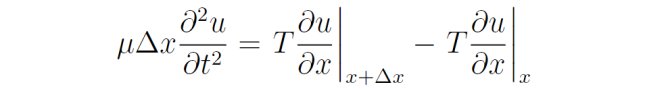
根据假设，T为常数，不依赖于x，对等式右边的偏导数做关于x的泰勒展开，并在消去一个Δx后让Δx趋向于0，最后得到：

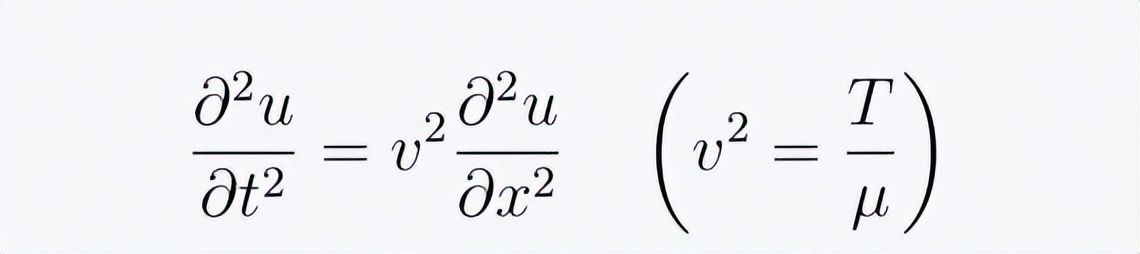
这就是琴弦的波动方程。由于时间关系，对于这个经典的微分方程，现场并未对其求解过程进行详细计算。张朝阳直接写出其通解的大致形式：

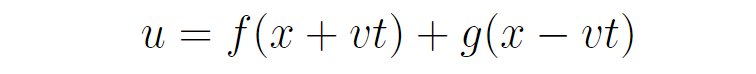
随后，他对这个通解作了进一步解释。以其中的g(x-vt)为例，假如函数g(x)的最大值点在x0处，那么在t时刻，g(x-vt)的最大值点在x-vt=x0处，也就是x=x0+vt处，即最大值点在以速度v向右运动。换言之，g(x-vt)表示向右以速度v传播的波。同理，f(x+vt)表示以速度v向左传播的波。经过这一番解释，波动方程中v的物理含义就清晰了，它代表波的传播速度。

在这个例子的最后，他还简短地讨论了两端固定的琴弦的波动方程。它本质上是一个边值问题，需要利用傅里叶级数展开的方法来求解，展开的每一项都是满足边界条件的一个模式。

推导空气中声音的波动方程：纵波与密度波

在声波方程的推导中，为了突出基本原理而避免陷入太琐碎的数学细节，本次课程只考虑了一维的情形，并且作了和琴弦类似的假设：静态时处于x位置的空气质点在声音过来时的位置偏移u(x,t)比较小，并且对空间坐标x的偏导数远小于1。

张朝阳介绍，声波是密度波，是一种纵波，质点的振动方向与传播方向平行，因此不像琴弦振动那样直观。不过，声波方程在数学推导上与琴弦的波动方程是比较类似的。考虑空气在(x,x+Δx)的“窄片”，“窄片”截面积是A，厚度为Δx。在水平方向上，“窄片”只受到气体的压力，根据牛顿第二运动定律可以得到：

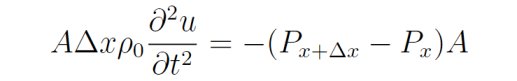
将上式两端的A消掉，并且将P对x做泰勒展开，消掉Δx并忽略高阶项可以得到：

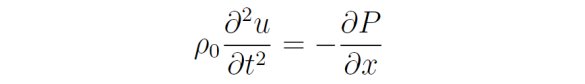
“是什么引起了压强的改变呢？答案是密度的改变。”因此，张朝阳转而考虑P 对密度ρ的依赖关系。假设没有声波时空气压强是P0，密度是ρ0，那么

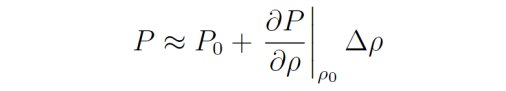
看到这里大家可能会疑问，这里P对密度的偏导数的准确定义是什么？根据理想气体物态方程，描述理想气体的状态需要两个物理量，而这两个量的选取具有任意性，因此必须明确这里P对ρ的偏导数是在保持哪个物理量不变的情况下的偏导数。对于这个问题，张朝阳后续又进行详细的解答。

文章来源：《大学物理》 网址: http://www.dxwlzz.cn/zonghexinwen/2022/0410/953.html